Difference between Rational and Irrational Numbers
A rational number is a number that can be expressed as the ratio of two integers, i.e. in the form of p/q, where p and q are integers and q is not equal to zero. Examples of rational numbers include -3/4, 0.25, and 22/7. They can be represented as a fraction, a decimal that terminates or repeats, and can be expressed as the ratio of two integers. On the other hand, an irrational number is a number that cannot be expressed as the ratio of two integers. These numbers cannot be represented as simple fractions, and when expressed as a decimal, the decimal representation is non-repeating and non-terminating. Examples of irrational numbers include √2, π, and e.
The key difference between rational and irrational numbers is that rational numbers can be expressed as a ratio of integers while irrational numbers cannot be expressed in that form.
In this article, you are going to learn a complete explanation of Rational vs Irrational Numbers.
This Article Also includes:
- Overview
- What is a Rational number?
- What is an Irrational number?
- Examples of both
- Lots more…!
So if you want to get benefits from this post you’ll love this post.
Let’s Dive right in…!
Overview
most people often confuse while identifying these numbers. the easy way to differentiate between both is that rational numbers and irrational numbers both are composed of integers but the first one can be written in p/q form and the last one cannot do so.
what does that mean by p/q?
for example, we have 6/3=2, which is a proper fraction. hence, it can be solved as p/q and is said to be a rational number. in another example, we have √11 which cannot be divided properly. hence √11 is an irrational number that cannot be written in p/q form.
Try Also: Difference between Trigonometry and Geometry
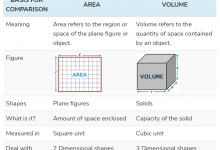
Difference between Rational and Irrational Numbers in Tabular Form
Rational | Irrational |
| those numbers can be written in form of p/q or a ratio of two numbers. | those numbers cannot be written in form of p/q or a ratio of two numbers. |
| for example 3/2= 1.5, 8.4, 6.6, etc. | for example √7=2.64, √11, etc. |
| they are always recurring in nature or finite. | they are always non-terminating and non-repeating in nature. |
| numerator and denominator belong to whole numbers and the denominator is not equal to zero. | they cannot be written in fractional form. |
| they are always perfect squares for example 4, 16, 25 25, 9, and so on. | they are always surds for example √2, √7, √11, √3, √5, and so on. |
What is a Rational Number?
The number consisting of integers that can be expressed in p/q form is known as a rational number. It is denoted by (Q) which lies in real numbers (R) while their participant integers (Z) are known as natural numbers (N). In this case, the integers consist of two parts denominator q, which cannot be zero, and numerator p.
every participant integer also belongs to rational numbers for example 7=7/1. the p/q expression ends with a finite number of digits or it shows a repeated pattern or sequence.
so, if the repeating or terminating decimal series is known as a rational number. similarly, the addition and multiplication of different integers of a rational number also turn into a rational number.
The terminology of Rational numbers
Rational numbers are numbers that can be expressed in the form of a ratio or fraction, p/q where p and q are integers and q is not equal to zero. The terminology used to describe rational numbers includes:
- Numerator: The number on top of the fraction that indicates how many parts are being considered.
- Denominator: The number on the bottom of the fraction that indicates the total number of parts in the whole.
- Simplifying or reducing a fraction: The process of making a fraction smaller by dividing both the numerator and denominator by their greatest common factor.
- Mixed numbers: A number that is a combination of a whole number and a fraction.
- Improper fractions: A fraction where the numerator is greater than or equal to the denominator.
- Proper fractions: A fraction where the numerator is less than the denominator.
- Reciprocal: The reciprocal of a fraction is found by flipping the numerator and denominator.
- Terminating decimal: A decimal representation of a rational number that ends at a certain point.
- Repeating decimal: A decimal representation of a rational number that repeats a certain set of digits indefinitely.
- Real numbers: All numbers including rational and irrational numbers.
It’s important to note that understanding the terminology related to rational numbers is essential to work with them in different mathematical operations and also helps in understanding more complex mathematical concepts.
What is an Irrational Number?
irrational numbers are those which are not rational and also belong to real numbers. these numbers cannot be expressed as the ratio of two integers. a common example of these numbers is √3, √2, etc. other than that, all square roots of natural numbers, other than of perfect squares, are irrational.
Try Also: