Greenhouse Effect definition causes and diagram

The term ‘Greenhouse Effect’ refers to the phenomenon in which certain gases (called greenhouse gases) trap heat 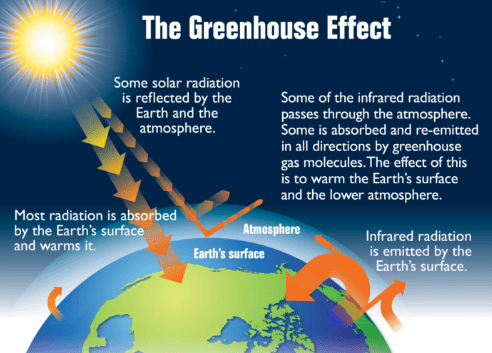in the atmosphere. These gases act like the glass in a greenhouse, which does not allow the inner heat to escape. When sunlight reaches the surface of the earth, much of its energy is transformed into heat energy.

Greenhouse Effect and Global Warming

The earth’s surface reflects this heat energy towards space as infrared radiation. The greenhouse gases trap infrared radiation and send it back to earth. Carbon dioxide, methane, and nitrous oxide are important greenhouse gases.

Global warming

In addition to greenhouse gases (e.g. carbon dioxide, methane, ozone) in the atmosphere increases the temperature of the earth. These gases remain in the lowest part of the earth’s atmosphere and do not allow solar radiation to reflect back into space. As a result, heats remain within the earth’s atmosphere and increases its temperature. This is called global warming.

Due to global warming, polar ice caps and glaciers are melting faster than the time taken for new ice layers to form. Seawater is also expanding causing sea levels to rise. Due to melting glaciers, rivers overflow and cause floods.

The CO₂ forms a layer around the earth like an envelope. It allows the heat rays of the sun to pass through it and reach up to the Earth. These rays are reflected from the earth’s surface and go back to the upper atmosphere. The normal concentration of the CO₂ layer retains enough heat to keep the atmosphere warm.

So, a normal concentration of CO₂ is necessary and beneficial for keeping the temperature warm. Otherwise, the earth would have been uninhabitable. The earth’s average temperature would be about -20⁰C, rather than the presently average temperature of 15⁰.

CO₂ is not an air pollutant. Rather, it is essential to gas for plants as O₂ is essential for animals. Plants CO₂ in the photosynthesis process and produce O₂. While animals use O₂ in respiration and give out CO₂. In this way, a natural balance exists between these essential gases as represented here.

But this balance is being disturbed by emitting more and more carbon dioxide into the air through different human activities.

Although carbon dioxide is not a poisonous gas, its increasing concentration due to the burning of fossil fuels in different human activities is alarming. CO₂ in the atmosphere acts like a glass wall of a greenhouse. It allows ultraviolet radiation to pass through it but does not allow infrared radiation to pass through it.

It traps some of the absorbed infrared radiations emitted by the earth’s surface that prevents heat energy from escaping from the atmosphere. It helps to stop the surface from cooling down at night. Therefore, the average temperature of the surface gradually increases. This is called the greenhouse effect.

This effect is proportional to the amount of CO₂ in the air. The greater the amount of CO₂ more is the trapping of heat or warming. The increased warming, this phenomenon is also called global warming.

Since 1800, the amount of carbon dioxide in the atmosphere has increased by 30%. The amount of methane has more than doubled and the amount of nitrous oxide has increased by about 8%.

Global weather monitoring scientists have reported that the temperature of the atmosphere of the earth is rising gradually. This increase in temperature is due to the greenhouse effect.

The name of the phenomenon is derived from a glass-built house or enclosure in which the plants are grown. Sun rays pass through the glass shields to reach the plants (for photosynthesis) but the heat coming from the sun cannot come out for the greenhouse and thus the temperature of the greenhouse rises.

Recently it is reported that the temperature of the atmosphere of the earth has risen 1 degree centigrade. This trend of temperature rise is called global warming.

The greenhouse effect is mainly caused by an increase in the number of greenhouse gases. Their gases are carbon dioxide, nitrous acid, methane, chlorofluorocarbons, and benzene in the atmosphere.

Scientists have estimated that the concentration of carbon dioxide in the atmosphere before the industrial revolution was between 275 and 285 parts per million and after it by 1980 it had risen to 338 parts per million. This increase is due to the burning of fossil fuels and the destruction of forests.

Even a very small amount of carbon dioxide produces an important greenhouse effect. Much of the solar radiation that reaches the surface of the earth is absorbed by the ground. As a result, the surface is heated up and it, in turn, emits its own radiation of a very long wavelength.

Atmospheric carbon dioxide acts as a shield to these heatwaves, so the same outgoing radiation is trapped, causing the earth’s surface to heat up still further. It has been estimated that the greenhouse effect warms the earth’s surface by as much as 15 degrees centigrade.

Almost all the radiation is sent back into space and the temperature does not rise. Actually, the earth is in a state of thermal equilibrium which keeps the surface temperature fairly constant. These equilibriums, however, disturbed the gradual increase in atmospheric carbon dioxide as a result of industrialization. It is noticeable that the highest intensity of the greenhouse effect is discovered on the planet, Venus.

The planet is wrapped in a thick blanket of carbon dioxide. It is not the planet nearest to the Su. Mercury is the planet nearest to the sun but it is not the hottest planet. Venus is the hottest planet with a surface temperature of 400 degrees centigrade. This high temperature is due to the greenhouse effect on the planet caused by its high concentration of carbon dioxide in its atmosphere.

Carbon dioxide is not the only gas to cause the greenhouse effect. Chlorofluorocarbons (CFCs) trap the heat 10,000 as carbon dioxide. They are mostly used in replaceable luxuries like air conditioners, perfumes, and fast food containers. They are also leading destroyers of the ozone layer in the upper atmosphere of the earth.

Alarmed by a series of droughts and heatwaves, a ban has been suggested on CFC production by the land of the century. It would probably cut greenhouse warming –after a lag- by up to 15%.

Effects of Global Warming

• The accumulation of carbon dioxide in the air is resulting in an increasing atmospheric temperature of about 0.05⁰C every year.
• It is causing major changes in weather patterns. Extreme weather events are occurring more commonly and intensely than previously.
• It melts glaciers and snowcaps that are increasing flood risks and intense tropical cyclones.
• Sea level is rising due to which low-lying areas are liable to be submerged, turning previously populated areas no longer habitable.

You May Also Like:

• Difference Between Environment and Ecology
• Carbon Cycle
• Photorespiration
• Gaseous Exchange in Plants
• What is Adenosine Triphosphate ATP?