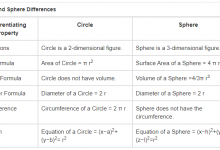
Types of Triangles

A triangle is a flat geometric figure (polygon) that has three sides. in simple words, the area closed by three lines is known as a triangle. it also has three angles and three vertices. Basically, there are six types of triangles which are as follows: Triangle Based on their Sides are isosceles, equilateral, scalene while Triangles Based on their Angles are obtuse, acute, and right. the sum of the angles of a triangle is equal to 180º.

so we can say that,

A Triangle has:

Sides: it has three and they are the lines that form the polygon.
Vertices: it has three and they are each of the points where two sides meet.
Angles: it has three and they are the openings that are formed when two sides join.

Note: we often use small letters like a,b, and c  to represent the sides and capital letters to represent the angles of different triangles. 

the triangles are known as simple polygons but are very helpful to understand the other complex polygon types.

Types of triangles according to their sides

1. isosceles Triangle
2. equilateral Triangle
3. scalene Triangle

isosceles Triangle

A triangle that has two equal sides also having equal opposite angles is known as the isosceles Triangle. this type of triangle satisfies the equation AB = AC then ∠B = ∠C. slice of pizza and a pair of earrings are real-life examples of such type.

Try Also: Isosceles Triangle

equilateral Triangle

The equilateral triangle is one that has all sides equal in length with all the angles have 60º. it is a regular polygon.

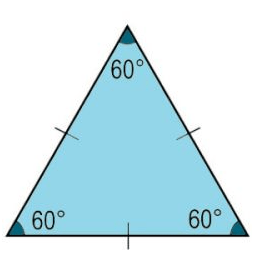
Try Also: equilateral Triangle

scalene Triangle

A scalene triangle is one that has neither equal sides nor equal angles.in other words, all the sides and angles are different from each other. but, the sum of all angles will always remain equal to 180 degrees.

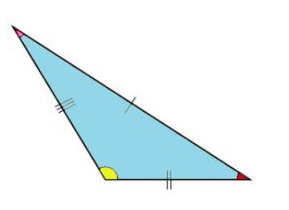
Try Also: Scalene Triangle

Types of triangles according to their Angles

1. obtuse Triangle
2. acute Triangle
3. right Triangle

obtuse Triangle

it one of the angles of a triangle is more than 90º, it is known as an obtuse-angled triangle. in this condition, the sum of the remaining two angles is less than 90°. we have some obtuse Triangle shaped roofs in our real-life examples.

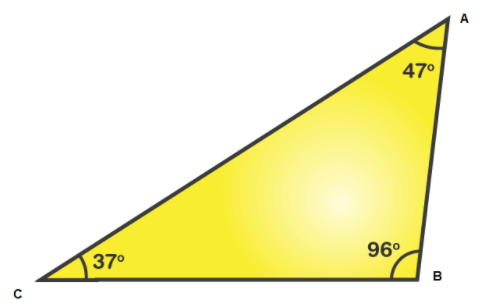
Try Also: Types of obtuse Triangle

Acute Triangle

if all the internal angles of a triangle are less than 90º, this type of triangle is called an acute triangle. it is a closed two-dimensional plane figure having three sides and angles. we can find the area of this triangle by using the formula = 1⁄2 Base X Height.

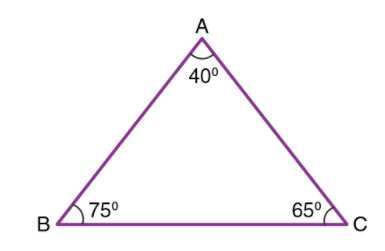
Try Also: Types of acute Triangle

right Triangle

Right triangles are those that are formed by a right angle and two acute angles. Therefore, the long side is the hypotenuse. For example, some isosceles and scalene triangles. This, however, can never happen with an equilateral triangle since the measure of its angles is invariable.

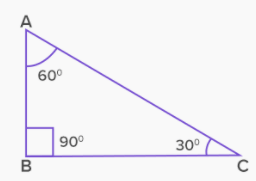
Try Also: Types of right Triangle

Properties of Triangles

1. One side of a triangle is less than the sum of the other two and greater than their difference.
2. The sum of the interior angles of a triangle is equal to 180 °.
3. The value of an exterior angle is equal to the sum of the two non-adjacent interiors.

FAQs (Frequently Asked Questions)

What are the 7 triangles?

equilateral, right isosceles, obtuse isosceles, acute isosceles, right scalene, obtuse scalene, and acute scalene are well-known seven types of triangles.

What are the 3 main types of triangles?

the three basic types of triangles based on the sides are equilateral, isosceles, and scalene.

What are the 4 types of triangles?

4 Triangle Types Are Isosceles, Equilateral, Obtuse, Acute, and Scalene.

What is a triangle and how many types of triangles?

A triangle is a polygon with three sides and three angles. there are 6 types of triangles of which three are based on angles and three are based on sides.

You May Also Like:

• Types of Quadrilaterals
• Types of Polygons
• Types of angles
• Complementary angles
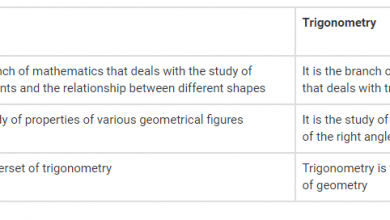
• Types of Trigonometry
• Types of Hexagon
• Types of Pentagon
• Difference between Length and Height